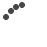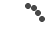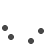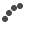Project: Enough analytics applies to matchings (elizabeth
25 май, 2023
g., crossing and you will nesting number). The fresh new crossing count cr(M) counts just how many minutes a pair of corners on complimentary mix. The newest nesting number for starters boundary matters the number of corners nested significantly less than they. The newest nesting matter for a corresponding ne(M) is the amount of the nesting wide variety for each and every line. Select the limit you can crossing and you can nesting quantity to own LP and you will CC matchings on the letter sides given that a function of npare this into maximum crossing and you can nesting wide variety having matchings which allow unlimited pseudoknots (named perfect matchings).
Project: We plus define right here a biologically driven fact known as pseudoknot amount pknot(M). A great pseudoknot takes place in a-strand out of RNA if strand folds for the itself and you will versions secondary bonds ranging from nucleotides, and therefore the exact same strand wraps to and you will models secondary securities again. not, when one pseudoknot has numerous nucleotides fused consecutively, we do not envision one to a beneficial “new” pseudoknot. Brand new pseudoknot number of a matching, pknot(M), matters just how many pseudoknots for the RNA theme from the deflating any ladders feeld online on the complimentary right after which finding the crossing number on ensuing complimentary. Such as for example in the Fig. step one.sixteen we offer one or two matchings that has hairpins (pseudoknots). Even in the event its crossing amounts each other equal six, we come across one inside Fig. step 1.16 A good, this type of crossing develop from a single pseudoknot, and therefore its pknot matter are step one, while in Fig. step one.16 B, the latest pknot count is step three. Discover limit pseudoknot amount on the CC matchings for the n sides once the a purpose of npare it on the limit pseudoknot number to the all perfect matchings.
Fig. 1.16 . One or two matchings which has had hairpins (pseudoknots), each having crossing numbers comparable to six, however, (A) possess one pseudoknot if you’re (B) features about three.
Search question: The fresh inductive process to have generating LP and you will CC matchings uses insertion off matchings ranging from several vertices due to the fact biologically that it is short for a strand away from RNA are inserted toward a preexisting RNA theme. Were there other biologically motivated strategies for doing large matchings from less matchings?
8.4 Brand new Walsh Turns
The new Walsh form try an orthogonal form and can be studied as reason for an ongoing or distinct changes.
Offered basic the fresh new Walsh means: that it form versions an ordered gang of rectangular waveforms that will simply take simply a couple viewpoints, +step one and you may ?1.
Viewing Analysis Using Distinct Transforms
The rows of H are the values of the Walsh function, but the order is not the required sequency order. In this ordering, the functions are referenced in ascending order of zero crossings in the function in the range 0 < t < 1 . To convert H to the sequency order, the row number (beginning at zero) must be converted to binary, then the binary code converted to Gray code, then the order of the binary digits in the Gray code is reversed, and finally these binary digits are converted to decimal (that is they are treated as binary numbers, not Gray code). The definition of Gray code is provided by Weisstein (2017) . The following shows the application of this procedure to the 4 ? 4 Hadamard matrix.
The first 8 Walsh characteristics are given within the Fig. 8.18 . It ought to be listed the Walsh features are going to be logically ordered (and you may listed) in more than just one-way.
Contour 8.18 . Walsh attributes on the variety t = 0 to at least one, when you look at the ascending sequency purchase from WAL(0,t), no no crossings to help you WAL(seven,t) having seven no crossings.
In Fig. 8.18 the functions are in sequency order. In this ordering, the functions are referenced in ascending order of zero crossings in the function in the range 0 < t < 1 and for time signals, sequency is defined in terms of zero crossings per second or zps. This is similar to the ordering of Fourier components in increasing harmonic number (that is half the number of zero crossings). Another ordering is the natural or the Paley order. The functions are then called Paley functions, so that, for example, the 15th Walsh function and 8th Paley function are identical. Here we only consider sequency ordering.